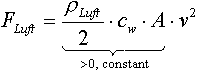
|
FLuft | Luftwiderstandskraft in [N] |
| ρLuft | Dichte der Luft, etwa 1,2 [kg/m³] | |
| cw | Luftwiderstandsbeiwert, dimensionslos | |
| A | Projizierte Stirnfläche des Fahrzeugs in [m²] | |
| v | Fahrgeschwindigkeit in [m/s] |
Die Theorie · Lösung mit der Gaußschen Fehlerquadratmethode · Berechnung mit Excel · Abweichung des Tachos
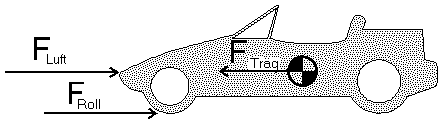
Neue Spezialreifen für den Geländewagen, Werbeversprechen über den cw-Wert des neuen Autos - aber stimmt das auch alles? Kann man den Luftwiderstand und den Rollwiderstand eines Autos (und damit vollmundige Werbeversprechen) ohne Windkanal und ohne aufwendige Technik prüfen?
Im Prinzip ja ! Sehen wir uns dazu einmal die wirkenden Kräfte im Bild an:
| Die Theorie |
Natürlich gibt es noch weitere Kräfte, z.B. die Reibung in den Radlagern und in Getrieben, die beim auskuppeln nicht von den Rädern getrennt werden, z.B. Gelenkwellen oder Differentialgetriebe. Aber die folgende Rechnung soll ja nur ein Beispiel geben, wie man den Luftwiderstand berechnen kann. Die Genauigkeit hängt u.a. auch von der verwendeten Messtechnik ab.
Der Luftwiderstand:
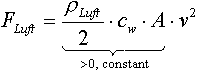
FLuft Luftwiderstandskraft in [N] ρLuft Dichte der Luft, etwa 1,2 [kg/m³] cw Luftwiderstandsbeiwert, dimensionslos A Projizierte Stirnfläche des Fahrzeugs in [m²] v Fahrgeschwindigkeit in [m/s]
Wie man sieht ist der Luftwiderstand -abgesehen von der Fahrgeschwindigkeit- nur von Werten abhängig, die sich während der Messung nicht ändern. Beim Rollwiderstand sieht die Gleichung so aus:
FRoll = mFz ⋅ g ⋅ kRoll FRoll Rollwiderstandakraft in [N] mFZ Fahrzeugmasse in [kg] g Ergbeschleunigung, etwa 9,81 m/s² kRoll Rollwiderstandsbeiwert, dimensionslos
Für unsere Berechnung wollen wir annehmen, daß nur diese beiden Kräfte das Ausrollen des Fahrzeugs bremsen. Um Rollwiderstand und Luftwiderstand zu bestimmen, ist folgender Versuchsablauf vorgesehen:
Unter diesen Randbedingungen läßt sich dann die Differentialgleichung der Bewegung nach Newton aufstellen:
mFz ⋅ a = - FLuft - FRoll
a, die Beschleunigung ist nichts anderes als die Änderung der Fahrgeschwindigkeit durch die Reibungskräfte, also a = dv/dt. Damit lassen sich alle Größen in die Differentialgleichung (DGL) einsetzen:
Nach einigen Umformungen erhält man:
Mit der eingezeichneten Vorzeichenanalyse ergibt sich auch der Lösungsweg dieser DGL. Mit einer Substitution kann man die Gleichung etwas übersichtlicher gestalten:
Bei der Auflösung der DGL wird eine Integration erforderlich. Die Grenzen ergeben sich aus dem Verlauf der Messung:
Die Integration führt auf die Lösung:
Wie man sieht, besteht die Formel zu einem großen Teil aus einem Ausdruck, der von der Anfangsgeschwindigkeit abhängt und für die Dauer des Ausrollens konstant ist. Mit dieser Formel kann man bei gegebenen Parametern (cw⋅A, kRoll...) jetzt also ausrechnen, welche Geschwindigkeit v(t) das Fahrzeug nach einer bestimmten Zeit t noch hat. Umgekehrt kann man diese Gleichung auch nutzen, um bei gegebener Ausrollzeit diese Konstanten zu berechnen.
Will man abwarten, bis das Fahrzeug steht, dann gilt die Bedingung v(tR) = 0 und es ergibt sich folgende Gleichung für das ausrollen.
Wenn man mehrere Messungen macht und die richtigen Parameter (cw ⋅ A, kRoll...) kennt, sollte die Gleichung -wie gezeigt- immer Null ergeben.
| Lösung mit der Gaußschen Fehlerquadratmethode |
In der Praxis werden sich allerdings Unterschiede ergeben, der tatsächliche Wert der Gleichung wird nicht Null, sondern ein kleiner Wert r sein, der in der Gaußschen Fehlerquadratmethode auch als Residuum bezeichnet wird:
Prinzipiell ist das Problem nichtlinear, die normale Gaußsche Fehlerquadratmethode bringt hier keine Lösung. Statt dessen muß iterativ eine Lösung gefunden werden. Das Gauß-Verfahren wird dazu modifiziert, das modifizierte Verfahren ist auch als Gauß-Newton-Verfahren bekannt.
Für dieses Verfahren sind einige mathematische Vorarbeiten erforderlich, denn das Residuum muß nach den gesuchten Parametern l und r partiell abgeleitet werden:
Daraus kann man jetzt ein Gleichungssystem zur Lösung formulieren:
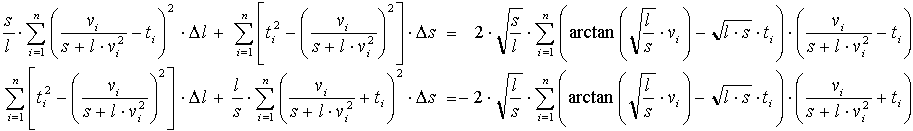
| So geht's in der Praxis |
Zugegeben, das ist jetzt mathematisch gesehen brutal hart - aber irgendwie muss man das Publikum ja beeindrucken und die Zweifler zum Schweigen bringen. Doch es geht auch ganz einfach, wenn man alles in einer Tabellenkalkulation verpackt. Dann kann jeder Hobbyanwender schnell ein paar Messungen durchführen und einen guten Hinweis für cw-Wert und den Rollwiderstand bekommen
Als einfache Hilfe habe ich eine Excel-Datei erstellt.
Die Datei enthält Makros, das sollte auch bei den Makro-Sicherheitseinstellungen von Excel berücksichtigt werden.
Diese Datei enthält eine Anleitung, wie man mit praktischen Fahrversuchen eine Tabelle aufstellt und eingibt.
Für den praktischen Versuch müssen folgende Voraussetzungen erfüllt sein:
| Wie genau ist der Tacho? |
Grundsätzlich gilt laut Straßenverkehrszulassungsordnung (StVZO) die Regel ‘Ein Tacho darf niemals weniger als die tatsächlich gefahrene Geschwindigkeit anzeigen’. Früher galt außerdem daß der Tacho nicht mehr als 7% über dem Skalenendwert anzeigen darf - geht der Tacho bis 200 km/h, darf er bis zu 14 km/h zuviel anzeigen) . Seit einigen Jahren gilt jedoch die Regel, daß ein Tacho nicht mehr als 10% der aktuellen Geschwindigkeit + 4 km/h anzeigen darf - bei 60 km/h also 10 km/h zuviel. Außerdem muß der Tacho Geschwindigkeiten in der Einheit km/h anzeigen.